原文参考 http://llimllib.github.io/pymag-trees/
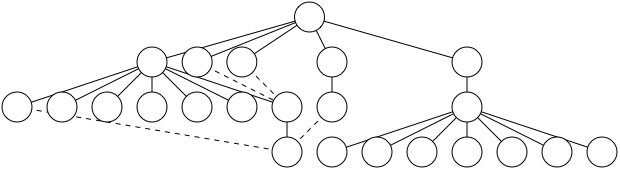
问题描述 给出一颗树,然后合理的可视化出来。具体来说,算法要求最后给每一个节点赋予一个坐标(x,y),使得这颗树画出来符合一些认知上的基本审美。为了存储计算结果,我们创建一个和原树镜像的数据结构。
1 2 3 4 5 6 class DrawTree (object) : def __init__ (self, tree, depth=0 ) : self.x = -1 self.y = depth self.tree = tree self.children = [DrawTree(t, depth+1 ) for t in tree]
随着我们画树的算法越来越高级,DrawTree也会越来越复杂,目前它只是吧所有x坐标置为-1,y坐标设为树的深度,每一个DrawTree的节点都有一个指向树根的引用。DrawTree的创建过程递归的为原树的每一个节点创造一个对应的包含额外绘制信息的DrawTree节点。
当我们在下文开始实现一些更好的算法之前,我们有必要利用我们的经验来建立一些原则来帮助我们去实现更好的算法。我们的目标是生成一颗好的树,所以这些原则能帮助我们定义什么是好的来指导改进我们的程序。
从Knuth开始 我们要画的东西的一个显然的特点是树的根节点在上,叶子节点在下。这种图,或者说这一类型的问题,归功于 Donald Knuth 为我们总结了两个原则:
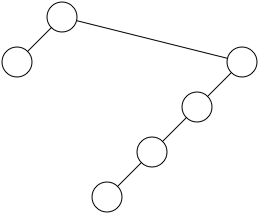
树的连接不能交叉 同样深度的节点应当在一条水平线,这样有助于让树的结构更清楚 Knuth的算法的优势在于非常的简单和高效,但是它只能工作在二叉树上,而且很多时候的结果并不好。它简单的中序遍历这颗树,使用一个全局计数器来递增每个节点的x坐标。
1 2 3 4 5 6 7 8 9 i = 0 def knuth_layout (tree, depth) : if tree.left_child: knuth_layout(tree.left_child, depth+1 ) tree.x = i tree.y = depth i += 1 if tree.right_child: knuth_layout(tree.right_child, depth+1 )
从结果看到,的确生成的树满足我们的原则,但不是很吸引人。你可以看到Knuth的图的宽度增长的非常快。因为我们从来不重用x轴上的多余空间,为了避免这种空间上的浪费,我们加入第三条原则:
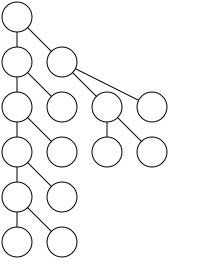
自底向上的方法 1979年,在Knuth介绍了树排版问题8年后,Charles Wetherell 和 Alfred Shannon 提出了一些创新的技术,满足了上述的三个原则。很简单,只要维护每一个深度目前有多少宽久可以了,自底向上,后序遍历。
1 2 3 4 5 6 7 8 nexts = [0 ] * maximum_depth_of_tree def minimum_ws (tree, depth=0 ) : tree.x = nexts[depth] tree.y = depth nexts[depth] += 1 for c in tree.children: minimum_ws(tree, c)
尽管她满足我们的原则,但是显然你会觉得这个结果是丑陋的。它很难体现出节点间的关系,所有的节点都被向左挤到一块了。所以我们需要再加入一个原则:
目前,我们只能侥幸的使用一些非常简单的算法来画树,因为我们还没有仔细考虑使用或者缓存一些局部的信息在节点上,比如目前我们几乎都是依赖于全局的计数器来保证节点不会相互重叠。为了满足父节点应当在居中于子节点的新原则,我们需要考虑在节点中加入新的context,一些新的策略是非常必要的。
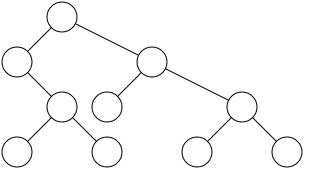
一种策略是Wetherell和Shannon在前文所述方法中,加入一个简单的操作,直接将父节点的x坐标使用子节点的坐标的的平均值。
在构建右树的过程中,我们需要时刻注意左树。右树有时候需要向右调整来为左边提供空间防止重叠。为了实现这样的分割,Wetherell 和 Shannon 维护了一个数组:每一层可用空间的开始位置,当居中父节点会导致右树和左树重叠时,使用开始位置来代替。
注: 需要向右偏移其实很好理解,假设你右树很深,下面生成出来都是很左边的位置,上面就会直接冲突。
使用mod来优化子树偏移 在我们看更多的代码之前,我们来仔细看看自底向上构件树的过程。我们会给每一个叶子节点一个可用的x坐标,如果它是分叉节点,我们就于子节点居中它。如果居中这个分叉节点,会导致重叠问题,那么我们就右移来避免冲突。
当我们把分支节点右移时,就不得不把整个子树全部右移,不然我们就不能保证父节点和子节点的居中关系。移动子树也是很容易的
1 2 3 4 def move_right (branch, n) : branch.x += n for c in branch.children: move_right(c, n)
这个能用,但是会带来新的问题,我们事实上会在放置节点这个递归调用中做移动子树这个递归调用,O(n) 变成了 O(n^2)。
为了解决这个问题,我们给每个节点一个额外的成员mod,当我们需要来到一个需要向右移动n单位的分差节点时,我们只将n加在自身的x坐标和mod上,但是不移动子树,然后继续愉快的向上构建。下次我们再把mod的调整一次应用在整个子树上。一旦第一次树遍历完成,我们就进行下一次树遍历来做右移的工作。这个仅仅是O(n)的开销,整体也是O(n)。
下面的代码是完整的居中节点,和移动子树的实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 from collections import defaultdictclass DrawTree (object) : def __init__ (self, tree, depth=0 ) : self.x = -1 self.y = depth self.tree = tree self.children = [DrawTree(t, depth+1 ) for t in tree] self.mod = 0 def layout (tree) : setup(tree) addmods(tree) return tree def setup (tree, depth=0 , nexts=None, offset=None) : if nexts is None : nexts = defaultdict(lambda : 0 ) if offset is None : offset = defaultdict(lambda : 0 ) for c in tree.children: setup(c, depth+1 , nexts, offset) tree.y = depth if not len(tree.children): place = nexts[depth] tree.x = place elif len(tree.children) == 1 : place = tree.children[0 ].x - 1 else : s = (tree.children[0 ].x + tree.children[1 ].x) place = s / 2 offset[depth] = max(offset[depth], nexts[depth]-place) if len(tree.children): tree.x = place + offset[depth] nexts[depth] += 2 tree.mod = offset[depth] def addmods (tree, modsum=0 ) : tree.x = tree.x + modsum modsum += tree.offset for t in tree.children: addmods(t, modsum)
注:使用mod来优化子树偏移其实就是因为上层的计算不需要所有的下层信息,只需要用一个变量来累计就可以,计算合并到一次进行。
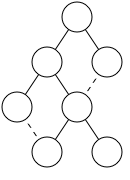
子树作为整体 尽管上述方法在很多情况下产生了很好的结果,但有些情况依然不尽如意(原文说它自己把图丢了…)。一个问题是:当一个相似的树结构,我们把它放在树的不同位置,画出来的效果可能会不一样。为了避免这个问题,我们从Edward Reingold和 John Tilford的论文中提取出新的一条原则:
尽管这样做会可能导致我们的图变得宽一些,但这样可以让我们的图传达出更多的信息。而且还可以帮助化简树的遍历过程:既然我们有一个子树的layout,相同的子树可以作为一个单位直接平移。
后序遍历树 如果是叶子节点,x坐标置0 如果不是或者放置它的右子树尽可能的不冲突的靠左 使用mod技术来优化子树移动 居中节点 二次遍历,展开mod 树轮廓
树的轮廓是指:关于树边缘的最大最小坐标列表。比如一个树的左轮廓,就是一个深度关于最左边起点位置的数组。右轮廓就是深度关于右边终点位置的数组。
如果我们把两颗树找到最紧密的位置结合在一起,我们需要找到左子树的右轮廓和右子树的左轮廓,根据这两个轮廓信息,找到需要将右树向右偏移的最小量。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 from operator import lt, gt // <= >=// 返回需要右移的大小 def push_right (left, right) : wl = contour(left, lt) wr = contour(right, gt) return max(x-y for x,y in zip(wl, wr)) + 1 // 生成轮廓 comp:比较函数 def contour (tree, comp, level=0 , cont=None) : if not cont: cont = [tree.x] elif len(cont) < level+1 : cont.append(tree.x) elif comp(cont[level], tree.x): // 如果是lt,那么就是最小的child,反之亦然 cont[level] = tree.x for child in tree.children: contour(child, comp, level+1 , cont) return cont
Threads
我们能够通过树轮廓的方法找到理想的右树偏移量。但是我们需要扫描子树来获得轮廓信息,使得算法退回到O(n^2)的效率。Reingold 和 Tilford 引入了一个新的概念叫 threads来解决这个问题(不是指多线程的threads)
threads 是一个通过 建立非父子的轮廓节点间联系 用来减少子树扫描轮廓次数的优化方法。另外我们依然能够利用一个事实: 如果一颗树比另一颗树要深,那么我们只需要检查较浅的一颗树的深度就够了,因为更深的树结构不会对它们如何更好的放在一起没有影响。
使用这种技术,并且只检查较浅深度的树轮廓,我们可以在线性时间里对子树计算轮廓和生成threads。
注:thread构建在下面
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 // 直接获得最靠右的节点 def nextright (tree) : if tree.thread: return tree.thread if tree.children: return tree.children[1 ] else : return None // 直接获得最靠左的节点 def nextleft (tree) : if tree.thread: return tree.thread if tree.children: return tree.children[0 ] else : return None // 这里不是算轮廓,是直接算偏移量 // 每一层靠thread直接拿下一层的左右树的最小最大x // 计算最大差值,浅的树走完,提早退出 def contour (left, right, max_offset=0 , left_outer=None, right_outer=None) : if not left_outer: left_outer = left if not right_outer: right_outer = right if left.x - right.x > max_offset: max_offset = left.x - right.x // lo:左树的左侧 li:左树的右侧 // ri:右树的左侧 ro:右树的右侧 lo = nextleft(left) li = nextright(left) ri = nextleft(right) ro = nextright(right) if li and ri: return contour(li, ri, max_offset, lo, ro) return max_offset
把所有东西组装起来 前面提到的轮廓方法暂时和前面提到的mod偏移技术不能一起使用,因为x坐标的真实值需要考虑所有父亲的mod,为了支持这种情况,我们修改一下轮廓的算法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 // 多添加了loffset和roffset来传递mod的偏移量 def contour (left, right, max_offset=None, loffset=0 , roffset=0 , left_outer=None, right_outer=None) : delta = left.x + loffset - (right.x + roffset) if not max_offset or delta > max_offset: max_offset = delta if not left_outer: left_outer = left if not right_outer: right_outer = right // lo:左树的左侧 li:左树的右侧 // ri:右树的左侧 ro:右树的右侧 lo = nextleft(left_outer) li = nextright(left) ri = nextleft(right) ro = nextright(right_outer) if li and ri: loffset += left.mod roffset += right.mod return contour(li, ri, max_offset, loffset, roffset, lo, ro) return (li, ri, max_offset, loffset, roffset, left_outer, right_outer)
固定子树位置和thread构建过程
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 def fix_subtrees (left, right) : li, ri, diff, loffset, roffset, lo, ro = contour(left, right) diff += 1 diff += (right.x + diff + left.x) % 2 // 右子树添加从轮廓计算的偏移量 right.mod = diff right.x += diff // if right.children: roffset += diff // thread 构建 if ri and not li: // 同级别结束的时候,如果左树的右侧存在,但是右树的最左没有 // 那么同级别左树的左侧的thread应该指向右树的左侧 // 因为这时候右树的左侧正好比左树低1 个深度 // 左树的左侧指向 右树的左侧 正好可以形成新的轮廓 lo.thread = ri lo.mod = roffset - loffset elif li and not ri: // 同理上面 ro.thread = li ro.mod = loffset - roffset return (left.x + right.x) / 2
在我们生成好轮廓之后,在左右子树最大差别处+1,来避免冲突。如果子节点是偶数,继续+1,使得父节点也可以放在整数位置。
当我们向右移动右树时,记住,我们不仅要把偏移量加载x坐标,还有右树自身的mod上,因为最后我们要做整个子树移动的。
如果左树比右树深,或者相反,我们需要加入thread,我们只要简单的检查一边的节点引用是否走的比另一边远,如果是,那么就从浅的根节点到深的根节点添加thread
为了能合适的处理之前说的mod值,我们需要设置一个特殊的mod值在threaded 节点上。既然我们已经计算出了右树的偏移量,那么我们只要设置thread节点的mod值为thread指向的节点和自身值的差就好了。
既然我们已经能够计算子树轮廓并且尽可能的放置在一起,我们就可以完整的实现整个算法,剩下的代码如下。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 def layout (tree) : return addmods(setup(dt)) def addmods (tree, mod=0 ) : tree.x += mod for c in tree.children: addmods(c, mod+tree.mod) return tree def setup (tree, depth=0 ) : if len(tree.children) == 0 : tree.x = 0 tree.y = depth return tree if len(tree.children) == 1 : tree.x = setup(tree.children[0 ], depth+1 ).x return tree left = setup(tree.children[0 ], depth+1 ) right = setup(tree.children[1 ], depth+1 ) tree.x = fix_subtrees(left, right) return tree
扩展到N叉树
注:简要总结一下,上面的方法用在n叉树上也是ok的,但是children的排列还不是很好,会被挤到左边。所以加入一条新的原则是children需要均匀排列。为了实现这样的均匀排列,需要考虑新的算法,调整最左树到最右树中间的一群子树的位置,使其相互不冲突。如果我们每次构建一层,然后逐个调整,就会和前面移动右子树一样,变成 O(n^2). 所以中间的树调整的偏移量需要一个和mod相似的办法缓存下来。重新均匀排列,并且缓存均匀排列的偏移量都不是问题。问题是均匀排列会造成新的冲突。
作者提供了一个sample code,看实现似乎是while里反复shift调整子树排列,写的非常trick。解释也没有提供太大帮助,这部分可能需要再参考其他实现继续研究。