QEM 网格模型简化算法

Posted on Apr 4, 2020

QEM 是一种常见和流行的网格简化算法。在阅读了一些源码和文章后特此笔记。

网格的简化是一个复杂的问题，与其全局的想怎么去简化不如从细节入手分而治之。从人的角度而言，手工简化其实也是针对基本图元的简单操作，即每次从网格上删除一个基本图元，一直迭代至满足要求。具体方法有：

顶点删除：从网格上一次移除一个顶点。移除后，网格上该顶点相关的面被删除，形成新的洞，再重新对这个洞三角化来补面。

边删除：从网格上一次移除一条边，塌陷这条边的两个顶点为一个。塌陷后再重新连接其他的面。

顶点合并：从网格上一次选择两个顶点进行塌陷，这两个顶点不一定需要构成边。塌陷后再重新连接其他的面。

QEM的方法适用于边删除和顶点合并的两种情况：都是把两个顶点合并成一个。后续只是连接性重建的问题。我的理解是边删除的方法能避免拓扑关系被破坏，而有些场景下，拓扑关系不是很重要，比如单纯用于渲染的mesh。而使用边删除因为拓扑的约束所以简模效果没有单纯的顶点合并来的理想。

什么是QEM

QEM是 Quadric Error Metrics的缩写。我先不直接解释这个东西是什么，先回归我们面对的具体问题：我们现在要从一个mesh上删除一条边。我们要选择哪一条边？我们选择的这条边，合并后的新顶点位置是什么？

我们其实只需要考虑后一个问题，因为我们在某个边上能找到的最佳点的质量就决定了这条边的质量，有了所有边的质量我们只需找到最好的就可以了，这就是边的选择的解法。

既然是网格简化，所以我们要尽可能保证每一步简化和原网格形状差别不大。考虑我们具体的操作是一个图元，所以这是个非常局部性的问题：当我们把一条边从网格上塌陷掉，在形状上的影响就是这条边原先所在的几个面的换成了新的几个面。具体而言就是：当合并前，我们有原先的两个顶点的位置，以及这些顶点周围的若干三角面。当合并后，我们有新的顶点位置，以及新的顶点周围若干三角面。

QEM方法的原则：就是合并后的这个顶点，应当到原先合并前两个顶点周围若干三角形所在平面的距离的平方和最小。有了这个原则，我们就可以计算给定网格上一条边，这个最优点在哪里，以及它有多优秀。

“到原先合并前两个顶点周围若干三角形所在平面的距离的平方和”，其实就是个函数 d = f(x, y, z)。这个函数在哪个xyz坐标取到最小值，这个坐标就是最优点的位置，这个最小值就是优秀的程度。

相信讲到这里，网格简化问题已经被说透彻了。而QEM本质上只是解决上面这个问题的数学工具。

对于一个三角面，其所在平面的方程有 ax + by + cz + d = 0。不难记得高中的几何知识：对于这种平面方程, 空间中任意一点到这个平面的距离就是直接把xyz代入就是，那么距离的平方的函数就是 d = (ax + by + cz + d)^2。那么所有平面的距离平方和就是把所有三角面的这个函数相加就是。然后再求个最小值就ok了。

Quadric 在数学上叫二次型。 d = (ax + by + cz + d)^2就是个二次型，所以我们就有展开后写成二次型矩阵的版本：

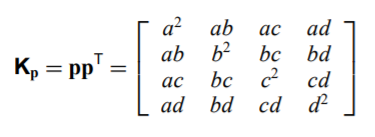
一旦这么写了以后，我们原先的这些平方和的函数，就变成的一堆矩阵的和，所以，对于某个顶点周围的三角面，我们只要用这个二次型矩阵就能表达空间中任一点到这些三角面距离平方和的函数。而这个矩阵，就是这个顶点的QEM。而对于我们上面讲到的“到原先合并前两个顶点周围若干三角形所在平面的距离的平方和”，那就是两个顶点的QEM矩阵和。

我的理解是用QEM存粹是工程上的考量，即便我不懂什么Quadric，我实际上也会实现上把平方和展开然后逐项存储，逐项求和。更有种用矩阵是为了简化运算的表示的意味。

不过在求最小值方面的确是不清楚不用二次型矩阵有什么更好的办法。